haveged - A simple entropy daemon
Runtime Testing
wikimedia image - hasnext.jpg
The haveged source tarball contains check targets to verify the correct operation using the included statistical tests. This verification is not available for binary haveged installs (although presumably performed by the package maintainer). This was always a little scary and the fact that it has worked well to date, is as much a testament to the generic nature of linux hardware as to the robustness of haveged.
With the advent of virtual machines, the assumption that a haveged binary built and tested on a particular architecture will behave similarly in a virtual environment is a more risky proposition. For example, there have been reports of VM that implement the processor time stamp counter as a constant and there are known differences in cpuid operation in others. The only real solution to this issue, is to incorporate run-time testing into haveged itself.
Testing Methodology
The IETF has written RFC4086, a 'Best Practices' document, detailing need for true randomness in cryptographic security. A number of standards bodies including NIST, ANSI, and ISO also have at least draft versions of standards related to random number generation. All of these standards classify Random Number Generators (RNG) as either deterministic (a 'DRNG') or non-deterministic (a 'NDRNG') with the DRNG class given considerably more coverage as evidenced by the following brief overview:
| FIPS-140, NIST SP800 | FIPS-140 provides a list of approved DRNG (NIST SP800-90) and recommendations for ensuring one of those RNG is properly implemented (a health test). There are no approved DRNG. In conjunction with FIPS-140, NIST also maintains a suite of statistical tests to verify the randomness of a RNG (SP800-22a). |
|---|---|
| ISO 18031 | Unlike NIST publications, ISO publications are copyrighted and not well suited to FOSF. What is known is that the ISO specification is similar to FIPS-140, but specifically targets NDRNG and related requirements, outlining the construction of NDRNG by combining an entropy source with a DRNG. The standard adds a continuous statistical test requirement of output to the generator health check requirements of FIPS-140. |
| ANSI X9.82 | The ANSI standard consists of Part 1 - Introduction, Part 2 - Entropy Sources, Part 3 - DRNG, Part 4 RBG construction. Similar focus to FIPS-140 and buried behind an unattractive pay wall. |
| BSI AIS20 and AIS-31 | BSI (Bundesamt für Sicherheit in der Informationstechnik), the German Common Criteria certification body, has long had evaluation standards for both DRNG (AIS-20) and NDRNG (AIS-31). |
As an 'unpredictable' RNG, the most obvious framework for evaluation haveged from the above list is AIS-31. This standard provides very, very high quality random numbers at the cost of high evaluation complexity.
Online testing is a central part of an AIS-31 evaluation. An AIS-31 device must implement a total failure test (a "tot" test) at device initialization and requires continuous testing of device output. The testing component is designed with the idea of allowing implementation with limited hardware resources and thus a suitable candidate for use in haveged run-time testing.
AIS-31 defines a standard statistical test suite to be used in evaluating a RNG and provides a reference implementation. The suite consists of 9 tests usually grouped into a 6 test group designed to check for statistically inconspicuous behavior (Procedure A), and 3 test group that is usually applied to the internal random bits of a TRNG (Procedure B). The AIS-31 test specification also includes recommendations for using the NIST test suite offline for additional analysis.
A colloquial description of the AIS-31 test suite follows.
| Procedure A | test0 is executed once on a 65536*48 bit sequence followed by 257 repetitions of test0 through test5 on successive 20000 bit sequences | |
|---|---|---|
| test0 | disjointedness test | 65536 48-bit strings are collected, sorted. No two adjacent values should be equal |
| test1 | monobit test [FIPS-140-1] | The number of ones must be between 9654 and 10346 |
| test2 | poker test [FIPS-140-1] | Distribution of 4 bit tuples checked for 15 degrees of freedom |
| test3 | runs test [FIPS-140-1] | Runs of 1, 2, 3, 4, 5, and 6 ones and zeros are checked for expected occurrences |
| test4 | longest run test [FIPS-140-1] | No single run can be larger than 34 |
| test5 | auto-correlation test | The overlap of the bit stream in the latter half of the sequence is compared to the sequence with the largest overlap in the first half of the sequence. Compute intensive |
| Procedure B | Distribution tests are conducted for widths of 1, 2, 4, 8 bits on successive samples followed by a single repetition of test 8 on a 256000 + 2560 bit sequence. Total sample size is depends on sample content. | |
| test6 | uniform distribution test | Test6a is a monobit test to ensure the number of ones is between 25% and 75% of total. Test6b is a special case of test 7 with a width of 2. |
| test7 | homogeneity test (comparative test for multinomial distributions) | Collect 10,000 occurrences of runs less than the given width and check for the expected transition probabilities. Test7a corresponds to a width of 3, Test7b corresponds to a width of 4. |
| test8 | entropy estimation (Coron's test) | Accumulate the nearest predecessor distance between byte values in a 256000 + 2560 bit sequence and calculate the empirical entropy. |
An ideal RNG was a probability of approximately 0.998 of passing either of the above procedures. In the case of a single failure, a retry is performed. For an ideal RNG, the probability that the retry fails is approximately 0.
haveged and AIS-31
While AIS-31 certification is not the goal of recent haveged development, it is useful to use the AIS-31 methodology to see how haveged stacks up against AIS-31 standards for a TRNG.
Early experimentation with AIS-31 attempted to fit haveged into AIS-31 as a sort of emulated TRNG. The tick counter data captured during the processor flutter measurements was run through AIS procedure B. Most samples failed all tests! On this data, test8 averaged approximately 6 bits of entropy per byte. However injecting the data into haveged always produced output that passed the procedure B tests.
This points out the crucial role played by the "walk" table in the HAVEGE algorithm. An XOR operation is used to combine timer readings with the walk table values selected by two pointers. The path of each pointer through the walk table is determined by a linear congruence relation based upon low order bits of the addressed data. The use of two pointers in the calculation approximates the mixing of two independent data sources using XOR. Further, each word in the walk table is the cumulative product of all preceding operations on that word. Generator warmup ensures that each walk table word is the product of at least 32 operations. The net result of the mixing multiple clock samples that takes place in the walk table removes the bias and merges the entropy of the clock samples so that the input passes procedure B.
This also means there is no clean separation of the internal noise source and internal data as in a true PTRNG. One AIS-31 PTRNG requirement is a theoretical model of the noise source. The earlier studies of processor flutter combined with the speculation above on how the walk table works its magic were not sufficient to constitute such a model.
Fortunately, the proposed AIS-31 version 2 specification introduced a new device class better suited to haveged. This class is called a Non Physical TRNG (NPTRNG), also known as a NTG.1 device. This is the same class as that given to the linux random number generator.
haveged as a NTG.1.2 Device
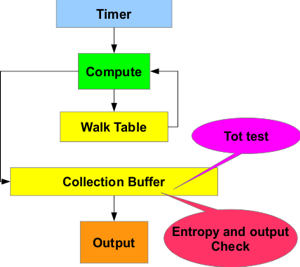
AIS-31 describes this device class as a non-physical TRNG with entropy estimation. The image at right shows haveged dressed as one of the device examples in the AIS-31 document with callouts showing the total failure (tot) and online tests required in such a device. Since there is no "raw" internal data, all tests are executed against the collection buffer contents immediately after a buffer fill. The tot test is executed against the buffer immediately after initialization. Continuous tests are executed after buffer fills triggered by data requests. In either case, a test can cleanly retry or fail the operation without risk of releasing data that does not meet the test requirements.
Using AIS-31 both test procedures A and B as a continuous test could meet all the requirements for the functional component specification for RNG.1.2 (NTG1.1 through NTG1.6) except for NTG1.4 (which is not currently specified).
In practice, some compromises need to be made:
- The two procedures are run serially on disjoint data. During continuous testing output data can be validated by running Procedure A or Procedure B singly or alternately. All tot tests must be passed for the generator to initialize successfully. Output will then continue as long as no continuous test procedure fails.
- There is no synchronization of testing data needs with the collection buffer. This means that test data will often span multiple buffer fills. During continuous testing, random data will be released from a buffer provided that the buffer contained no single failed test. If the buffer contains any test failure, the buffer will be refilled as necessary until the current test completes in a successful retry or test failure. Output will resume with the refilled buffer after a successful retry.
- Procedure A contains an auto-correlation test, test5, that is several orders of magnitude slower than any other individual test. This test is member of the procedure A tests that is repeated 257 times during the test. Because this performance will not be acceptable in some circumstances, procedure A has been modified to skip test5 during some repetitions - all other tests are performed. The modified procedure A are labelled A1 through A8 where A<n> indicates that test5 is skipped every 2^n repetitions during procedure A
For those building haveged from source, the following table compares the existing nistest implementation with the AIS-31 recommendations.
| Test | Configuration item | Recommendation | nistest |
| All tests | Bits per sequence | 1000000 | 1000000 |
| Number of sequences (sample size) | 1073 | 108 | |
| Frequency Test within a Block | Block Block length | 20000 | 2^(7-24) |
| Non-overlapping template test | Template length | 10 | 9 |
| Overlapping template | Block length | 10 | 9 |
| Maurer's "Universal Statistical" test | Test block length L | 7 | 6-13 |
| Initialization steps | 1280 | 2^L * 10 | |
| Approximate Entropy Test | Block length | 8 | 3-16 |
| Linear Complexity Test | Block length | 1000 | 4713 |
| Serial Test | Block length | 16 | 14 |
Hyphenated values for nist values indicate iteration. The nistest suite also includes runs, max runs, binary matrix rank, discrete Fourier transform, csum, and random excursion tests from the NIST test suite.
Current NIST practice emphasizes more thorough testing on a smaller sample. Since the NIST test suite is already a burden on some platforms, no change is currently anticipated.
Using haveged runtime Testing
Not everyone needs full NTG1.2 security and haveged provides a command line option to adjust the level of testing to suit any particular needs. The -o option provides complete control over all tests executed continuously or at start up. The option consists of a case insensitive string of up to two terms "[c,t][a[1,8]][b]" where
- [c,t]
- indicates the continuous or tot section
- [a[1,8]][b]
- indicates that procedure A variant and/or procedure B should be run
The resource cost of the testing component is near zero with all tests disabled ("ct"), and increases only as necessary for the tests enabled. For those on a very tight resource budget and building from the source distribution, the entire test facility can be suppressed in the build (--disable-olt).
Because no special hardware is involved other than the CPU, the tot test is probably sufficient for ensuring haveged is operating correctly under all but the most critical conditions. Continuous testing will introduce a noticeable performance penalty. In terms of performance, procedure B is lighter weight than Procedure A even with the lightest test5 variant (the "a8" option runs test5 only twice during the procedure).
The following table illustrates the relative performance costs of the testing options on Fedora 17.
| command | user | system | elapsed | note |
|---|---|---|---|---|
| haveged -n 16m -o tc | 0.13 | 0.10 | 0.41 | no tests run |
| haveged -n 16m -o tbc | 0.19 | 0.09 | 0.45 | tot test b |
| haveged -n 16m -o ta8bc | 0.34 | 0.08 | 0.58 | tot test lightweight a, test b |
| haveged -n 16m -o ta8bcb | 0.51 | 0.08 | 0.78 | as above with continuous test b |
| haveged -n 16m -o tba8cba8 | 1.28 | 0.07 | 1.54 | as above with continuous lightweight a |
| haveged -n 16m -o tabc | 10.83 | 0.08 | 11.07 | tot with full a and b |
| haveged -n 16m -o tbacab | 77.28 | 0.09 | 1:17 | as above with continuous full a and b |
The supplied default values for run time tests are:
- ta8bcb
- when run as daemon
- ta8b
- when run as application
Procedure B is run continuously in the daemon case to ensure the empirical entropy is near the 8 bits/byte estimate passed into the random device. The performance penalty for other continuous tests is probably not critical because the random device perorms its own mixing of the entropy pool.
As a practical suggestion, testing results are very unlikely to vary on most installations since no external hardware is involved. Once an installation has proven itself on a host, test options can be modified for better performance as desired.